Mathematisches Intermezzo zum Astrolabium
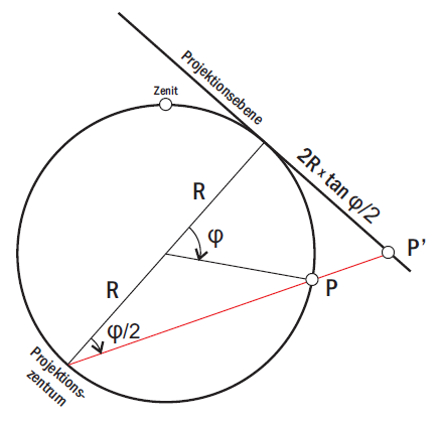
Bislang konnte geometrisch, d.h. mit Zirkel und Lineal konstruiert werden. Es geht aber auch arithmetisch über die Umrechnung von Koordinaten. Extrem einfach ist die Formel für Kugelkoordinaten (R, φ, α), wobei R der Radius der Kugel, φ Winkel zur Projektionsachse und α der Azimutwinkel ist.
Letzterer beschreibt die Drehung um die Projektionsachse und bleibt wegen der Winkeltreue bei der Abbildung erhalten. Der Bildpunkt P' hat dann die Entfernung 2R ˟ tan φ/2 von der Projektionsachse. Der Winkel φ/2 ergibt sich, weil das Dreieck 2 gleiche Schenkel und damit 2 gleiche Winkel hat; der dritte Winkel ist 180 - φ.
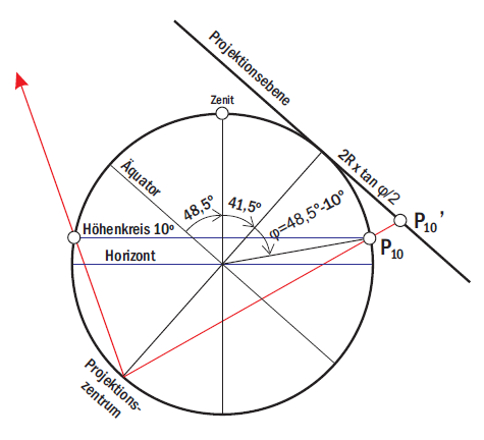
Für die auf der Vorseite konstruierten Höhenkreise ergibt sich
φ = 48,5 - 10 = 38,5 tan 19,25 = 0,349
φ = 48,5 - 20 = 28,5 tan 14,25 = 0,253
φ = 48,5 - 30 = 18,5 tan 9,25 = 0,163
etc.
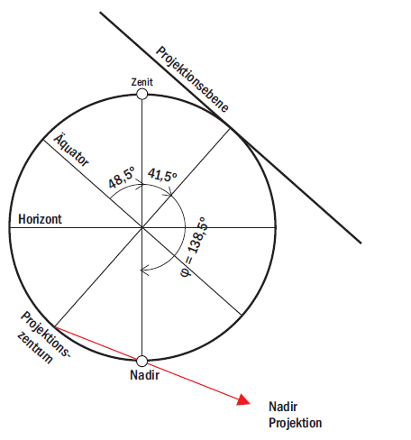
Die Formel gilt auch für φ ˃ 90°. Etwa für den Gegenpol des Zenits, den sogenannten Nadir:
φ = 180° - 41,5° = 138,5°.
Die Entfernung von der Projektionsachse beträgt 2R ˟ tan 69,25° = 2R ˟ 2,63945.
